Xavier Gonzalez, Andrew Warrington, Jimmy T.H. Smith, Scott W. Linderman
This paper builds on previous work, which showed that a non-linear RNN forward pass of length L does not need to be evaluated sequentially. Instead, all L states can be evaluated concurrently.
By formulating the evaluation of the RNN as a non-linear least squares problem, a starting state can be given and the remaining states can be iteratively refined in parallel by minimizing the objective, as shown in Figure 1 from the original paper.
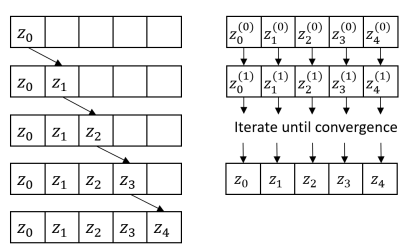
Figure 1 from Parallelizing Non-linear sequential models over the sequence length
The authors of this paper noted that the method of solving the non-linear least squares problem in the previous work was unstable and can easily fail to converge.
The method (Gauss-Newton) works by iteratively linearizing the non-linear residual around the current solution and solving the least squares problem to get a new estimate of the solution. If the residual function has sufficiently high curvature, this linear approximation will be poor and cause the optimization to fail to converge.
The authors instead propose using the Levenberg-Marquardt algorithm which adds a “trust region constraint” that stabilizes the objective. This augments the objective with a penalty for solutions too far away from the previous one. Essentially, it says that the linearization is only accurate within a certain radius of the previous solution. This prevents the optimization from taking steps that are too large and causing the objective to diverge.
The authors also propose quasi-newton methods by noting the particular structure of the matrix involved in the optimization problem allows them to approximate the Jacobian and thus obtain much faster optimization.
RNNs are a classic example of inherently sequential models, so it is notable that algorithms from optimization can reframe the problem so fundamentally.
Towards scalable and stable parallelization of nonlinear RNNs